Wiener–Khinchin theorem
The Wiener–Khinchin theorem (also known as the Wiener–Khintchine theorem and sometimes as the Wiener–Khinchin–Einstein theorem or the Khinchin–Kolmogorov theorem) states that the power spectral density of a wide–sense stationary random process is the Fourier transform of the corresponding autocorrelation function.[1][2][3][4]
Contents |
History
Norbert Wiener first published the result in 1930, Khinchin independently later in 1934. Einstein had anticipated the idea in a brief two-page memo in 1914.[5]
Continuous case
For the continuous case:
where
is the autocorrelation function (also called autocovariance) defined in terms of statistical expectation, and where 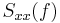 is the power spectral density of the function
is the power spectral density of the function 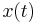 . Note that the autocorrelation function is defined in terms of the expected value of a product, and that the Fourier transform of
. Note that the autocorrelation function is defined in terms of the expected value of a product, and that the Fourier transform of 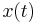 does not exist in general, because stationary random functions are not square integrable.
does not exist in general, because stationary random functions are not square integrable.
The asterisk denotes complex conjugate, and can be omitted if the random process is real-valued.
Discrete case
For the discrete case:
where
and where 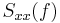 is the power spectral density of the function with discrete values
is the power spectral density of the function with discrete values ![x[n]\,](/2012-wikipedia_en_all_nopic_01_2012/I/b0f955b87baf7377b98b47ed9c723949.png) . Being a sampled and discrete-time sequence, the spectral density is periodic in the frequency domain.
. Being a sampled and discrete-time sequence, the spectral density is periodic in the frequency domain.
Application
The theorem is useful for analyzing linear time-invariant systems, LTI systems, when the inputs and outputs are not square integrable, so their Fourier transforms do not exist. A corollary is that the Fourier transform of the autocorrelation function of the output of an LTI system is equal to the product of the Fourier transform of the autocorrelation function of the input of the system times the squared magnitude of the Fourier transform of the system impulse response.[6] This works even when the Fourier transforms of the input and output signals do not exist because these signals are not square integrable, so the system inputs and outputs cannot be directly related by the Fourier transform of the impulse response.
Since the Fourier transform of the autocorrelation function of a signal is the power spectrum of the signal, this corollary is equivalent to saying that the power spectrum of the output is equal to the power spectrum of the input times the power transfer function.
This corollary is used in the parametric method for power spectrum estimation.
Discrepancy of definition
By the definitions involving infinite integrals in the articles on spectral density and autocorrelation, the Wiener–Khinchin theorem is a simple Fourier transform pair, trivially provable for any square integrable function, i.e. for functions whose Fourier transforms exist. More usefully, and historically, the theorem applies to wide-sense-stationary random processes, signals whose Fourier transforms do not exist, using the definition of autocorrelation function in terms of expected value rather than an infinite integral. This trivialization of the Wiener–Khinchin theorem is commonplace in modern technical literature, and obscures the contributions of Aleksandr Yakovlevich Khinchin, Norbert Wiener, and Andrey Kolmogorov.
Notes
- ^ Dennis Ward Ricker (2003). Echo Signal Processing. Springer. ISBN 140207395X. http://books.google.com/books?id=NF2Tmty9nugC&pg=PA23&dq=%22power+spectral+density%22+%22energy+spectral+density%22&lr=&as_brr=3&ei=HZMvSPSWFZyStwPWsfyBAw&sig=1ZZcHwxXkErvNXtAHv21ijTXoP8#PPA23,M1.
- ^ Leon W. Couch II (2001). Digital and Analog Communications Systems (sixth ed. ed.). Prentice Hall, New Jersey. pp. 406–409. ISBN 0135225833.
- ^ Krzysztof Iniewski (2007). Wireless Technologies: Circuits, Systems, and Devices. CRC Press. ISBN 0849379962. http://books.google.com/books?id=JJXrpazX9FkC&pg=PA390&dq=Wiener-Khinchin-Einstein&ei=1SxlSPGhB4jgsQPr5b3lDw&sig=ACfU3U2Phnk-zwJi57XrvNmdfosyg55FVA.
- ^ Joseph W. Goodman (1985). Statistical Optics. Wiley-Interscience. ISBN 0471015024.
- ^ Jerison, David; Singer, Isadore Manuel; Stroock, Daniel W. (1997). The Legacy of Norbert Wiener: A Centennial Symposium (Proceedings of Symposia in Pure Mathematics). American Mathematical Society. p. 95. ISBN 0821804154.
- ^ Shlomo Engelberg (2007). Random signals and noise: a mathematical introduction. CRC Press. p. 130. ISBN 9780849375545. http://books.google.com/books?id=Zl51JGnoww4C&pg=PA130.
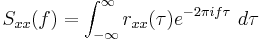
![r_{xx}(\tau) = \operatorname{E}\big[\, x(t)x^*(t-\tau) \, \big] \](/2012-wikipedia_en_all_nopic_01_2012/I/5adde582dea293fa3563f66d401ff0b9.png)
![S_{xx}(f)=\sum_{k=-\infty}^\infty r_{xx}[k]e^{-2\pi i k f}](/2012-wikipedia_en_all_nopic_01_2012/I/43070489697147c77532bead8b95e8c9.png)
![r_{xx}[k] = \operatorname{E}\big[ \, x[n] x^*[n-k] \, \big] \](/2012-wikipedia_en_all_nopic_01_2012/I/5b483d0d1141ae20b33ce3e99958aa8d.png)